A importância do cálculo mental para a construção do conceito de número

A importância do cálculo mental para a construção do conceito de número

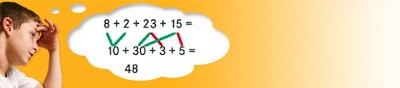
O cálculo mental ajuda a compreender o sistema de numeração e as propriedades das operações.

Muitas crianças são dotadas de uma inteligência lógico matemática e são capazes de resolver problemas matemáticos, fazer contas e falar a tabuada mais rápido do que outras que estariam usando uma calculadora por exemplo.

É importante estimular os alunos a usar a mente e o raciocínio lógico, mas não devemos nos esquecer que cada criança tem uma necessidade diferente em cada disciplina e devemos respeitar o tempo destas.

No dia-a-dia, nem sempre é necessário chegar ao valor exacto ao final de uma conta. Na maioria das vezes, basta uma aproximação para tomar uma decisão: o dinheiro vai dar para comprar tudo o que preciso na cantina da escola? A quantidade de pacotes de cadernos vai ser suficiente para toda a turma? Arredondar pode ser útil em situações como essas.

Reservar um tempo para o confronto das diferentes estratégias faz com que a criança analise outras maneiras de resolver as contas e se aproprie das que lhe parecem mais eficazes. Conforme os estudantes vão contando o raciocínio desenvolvido, você pode registar as etapas no quadro para que o resto do grupo acompanhe. Diferentemente do que pode parecer, a escrita não é proibida no cálculo mental.

A escrita dos cálculos e as técnicas operatórias

ASIMOV, Isaac. No mundo dos números. Rio de Janeiro: Francisco Alves, 1995

Para o matemático Issac Asimov, parece simplesmente que os números inteiros são formados começando por um, adicionando mais um, e assim por diante. Afinal, por maior que um número seja mesmo que ele se estenda em série de pequenos números daqui até a estrela mais distante, é sempre possível dizer "esse número mais um" e obter um número ainda maior. Contudo, boa parte do que hoje se chama matemática deriva de ideias que originalmente centravam-se nos conceitos de número, grandeza e forma. E, a aprendizagem acontece da maneira mais natural e possível. Issac, quer dizer que a matemática é simples e abrangente ao mesmo tempo, pois é uma ciência que se difere de todas e está inserida em nossas vidas.

KAMII, Constance. A criança e o número. Campinas: Editora Papirus, 2000.

Segundo um dos grandes estudiosos, Constance KAMII, o ensino de matemática tem que ser livre, ou seja, a aprendizagem tem que acontecer de maneira interactiva e autónoma. Sendo assim, o aluno poderá se interessar naturalmente pelos cálculos, e com os estímulos recebidos pelas aulas presenciadas consiga desenvolver e construir seu pensamento crítico, raciocínio lógico e o cálculo mental.

O livro de Constance Kamii aborda os processos envolvidos na construção do conceito de número pelas crianças e ajuda o professor a observar como elas pensam a fim de entender a lógica existente nos erros.

Constance defende que, diferentemente do que algumas interpretações indicam, desenvolver e exercitar os aspectos lógicos do número com atividades pré-numéricas (seriação, classificação e correspondência termo a termo) é uma aplicação equivocada da pesquisa de Jean Piaget (1896-1980), preocupações epistemológicas e não didácticas. Sabe-se que as noções numéricas são desenvolvidas com base nos intercâmbios dos pequenos com o ambiente e, portanto, não dependem da autorização dos adultos para que ocorram. Ninguém espera chegar aos 6 anos para começar a perguntar sobre os números. A criança ativa e curiosa não aprende Matemática memorizando, repetindo e exercitando, mas resolvendo situações-problema, enfrentando obstáculos cognitivos e utilizando os conhecimentos que sejam frutos de sua inserção familiar e social.

20 situações em que usamos a Matemática

Às vezes os alunos perguntam “Quando estarei a utilizar a matemática? ” “Para que resolver estes problemas? ” “Temos calculadora, para que aprender a fazer contas? ”

Para estas perguntas temos infinitas respostas, as quais colocarão os alunos a par da matemática em seu dia-a-dia. Por exemplo:

1 - Realizar compras no supermercado;
2 - Comprar pães na padaria;
3 - Dividir um doce com o amigo;
4 - Na cozinha fazendo uma receita;
5 - Para saber a altura que conseguimos pular;
6 - Para ver as horas no relógio;
7 - Para saber a distância da nossa casa até a escola;
8 - Para comprar determinada quantidade de carne no açougue, exemplo meio quilo;
9 - Para calcular gastos mensais, como água e luz;
10 - Para medir uma parede ou imóvel;
11 - Para solicitar desconto em alguma compra;
12 - Brincando com jogos com os amigos;
13 - Para fazer uma dieta;
14 - Abastecendo o carro no posto de gasolina;
15 - Quando vamos fazer compras e temos uma certa quantia para gastar;
16 - Dividindo tarefas no serviço de casa;
17 - Para pagar a passagem do ônibus;
18 - Para usar o telefone;
19 - Calcular a nota na escola;
20 – Para mudar um móvel de lugar, necessitando verificar o espaço.

Quando já se apropriaram dos conceitos básicos da matemática, os alunos, ao chegarem aos últimos ciclos da Educação Infantil, começam a ter um contacto mais directo com as operações matemáticas, como adição e subtracção. Ao mesmo tempo, os educadores começam a inserir nas práticas em sala de aula a representação dos números.

Neste momento de descobertas, é importante que os contextos pedagógicos, bem como as ações em casa, sejam baseados em práticas do cotidiano do pequeno, como a organização de objectos na classe ou no quarto, jogos, uso do calendário e contacto com o relógio para ver as horas.

Essa abordagem lúdica é muito mais efectiva do que apresentar os conteúdos de forma dirigida para criança, que vê muito mais sentido quando o aprendizado é aplicado em seu dia-a-dia. Por isso, é fundamental estimulá-las por meio da brincadeira a pensarem e a irem em busca de suas próprias descobertas matemáticas, na escola e em casa.

Texto de Agnes Raunaimer, Ariana Almeida, Daniela Silva, Ionne Marques

Adaptado por Eliane Zulian Delázari

http://descompliqueamatematica.blogspot.com/

http://www.reforcoescolarinstruir.com.br